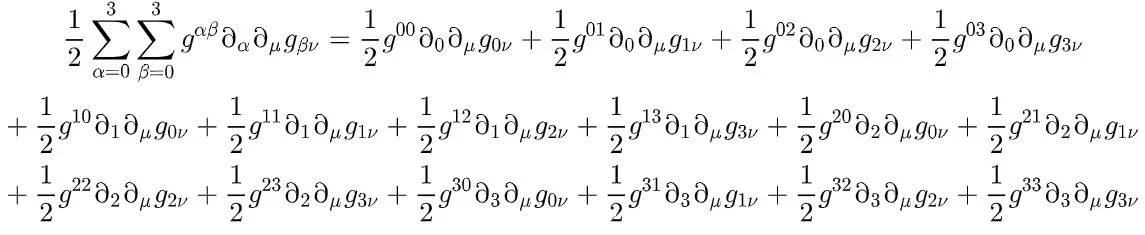general relativity and quantum mechanics

[TimeWalker0100001]

Could someone explain to me better how the union of quantum mechanics with general relativity works???? and why it is so debated among physicists today??

 

[Darby]

Could someone explain to me better how the union of quantum mechanics with general relativity works???? and why it is so debated among physicists today??

Well, first, it doesn't work. When physicists attempt to frame gravity in terms of quantum mechanics the equation "blows up." The solutions lead to mathematical singularities, infinities, divide by zero answers - solutions that are not observed in the real world. The solutions are wrong. I don't know if it is a matter of debate. It's a search for the solution to the question of how does gravity fit into quantum mechanics? Why is it so difficult to solve after almost 115 years? Here's an example:

This is the equation for General Relativity - Gμν+Λgμν=c48πGTμν

But that's a very condensed form. The first term is G sub meu neu. It's the gravitational part of General Relativity. Here's the full expansion of G meu neu term:



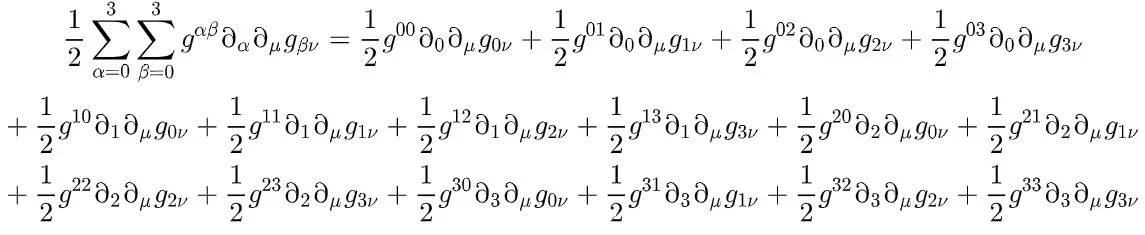
And remember. This is just the first term. To solve the equation you have to fully expand every term. And look at the backwards "Q's". Those indicate "partial differential". It is only solving for one axis for one independent variable that is part of four dimensional spacetime. You still have to deal with the cosmological constant lambda gee meu neu portion of the equation. That's the force that causes the universe to expand against gravity. That equation is equally daunting. And then as to both you have to do each of them three more times to account for the x, y, z and t axes.

So the equation is huge. Really huge. The math expertise and training to work the problem is also huge. And no one actually knows what the exact value of the cosmological constant is. That means there are literally an infinite number of possible solutions to general relativity...and we still can't fit gravity into quantum mechanics.

Why is gravity so hard to fit it in? One reason is that we know that at huge distances gravity dominates all the other forces. The universe is electromagnetically neutral when you look at it in large scale. The strong and weak forces don't affect the large scale because they aren't felt outside of an atom's nucleus. But at the scale of an atomic nucleus gravity is so weak that it can be completely ignored. If we assign a strength of 1 to gravity then the strength of the strong force is:

100,000,000,000,000,000,000,000,000,000,000,000,000 (10^41)

Gravity is 10^41 times weaker than the strong force. The electromagnetic force is 10^39 times greater.

 

[TimeWalker0100001]

interesting

 

[Darby]

Oops! I didn't get enough zeroes in that number. Here's the correct 10^41:
100,000,000,000,000,000,000,000,000,000,000,000,000,000

Gravity is 10^41 times weaker than the strong force. The electromagnetic force is 10^39 times greater

And that's a bit confusingly stated. It should be:

"If we set the strength of gravity to 1 then the relative strength of the strong force is 10^41. The relative strength of the EM force would be 10^39."

You can see why gravity is ignored in nuclear physics. Inside the atomic nucleus the strong force and EM battle for dominance but gravity has absolutely no effect on the interior workings of a single nucleus. And where does quantum physics live? Among other "places" it lives in and dominates the inner workings of the nucleus of atoms. It's pretty hard to incorporate gravity (General Relativity) into QM if gravity is completely ignored at the quantum scale.